|
E fejezet elején rögzíteni kell, hogy a favázas épületek méretezése komoly felkészültséget igénylő, szakértő statikus által végzendő munka. De annak, akit érdekel e téma, nem válik kárára, ha megismeri azokat a szabályokat, lehetőségeket, melyek a fachwerk építkezés alapszabályai közé tartoznak - és melyek ismerete segít a szándékok megvalósításában. A fachwerk stílusú építészet több évszázadon át alakult ki. A régi mesterek elődeik által kidolgozott, hol írásos, hol csak szóbeli hagyomány alapján szerkesztették, alkották meg házaikat. Egészen az XIX-XX. század fordulójáig nem is igazán használatos a maihoz hasonló statikai, számítási eljárás a hagyományos (értsd: fa, tégla, kő) szerkezetek méretezésére. Maga az építészeti statika is csak a XIX. század második felében a vas, majd a vasbeton építészeti használatával egyidejűleg fejlődött ki, ezért természetszerűleg jobbára ezen anyagokkal foglalkozott. A faanyagok, faszerkezetek tervezésénél, építésénél a sok száz éves hagyományokat, szabályokat követték, nem látták szükségét annak, hogy külön statikai számítások készüljenek a faanyagok felhasználására. A XIX sz. nagy ipari, építési fellendülése volt, ami a pontos méretezés szükségességét megkövetelte, de közrejátszottak ebben az akkor még sokfelé dúló háborúk is. Elsősorban az alapanyagínség (a háború, a szankciók miatt nem lehetett minden építési anyaghoz hozzájutni), másrészt az, hogy a háborúban megsemmisült építmények, műtárgyak gyors újjáépítésére (gyakran rövid időn belül újabb és újabb újjáépítésére) volt szükség. Nem véletlen tehát, hogy még a XX. század elején is a szakemberek nem számítások alapján szerkesztették meg a fatartókat (legyenek azok fedélszékek részei, vagy éppen a favázas épület oszlopai), hanem a tapasztalati úton nyert szabályok szerint. A korábban már idézett 1904-es építészeti szakkönyv az alábbiakat rögzíti a favázas téglafalak (azaz a fachwerk) favázainak méretezéséhez
Előírások egy 1904-es szakkönyvből
Statikai alapelvek laikusok számára A testek, szerkezeti elemek Az erők A testek viselkedése erők hatására Elemek szilárdsága, határfeszültségek Statikai-tartószerkezeti számítások elmélete, menete Kiindulási adatok Födémgerenda tervezése Konzolok Koszorúgerenda méretének számítása A faváz oszlopainak méretezése Talpgerendák méretezése Falak méretezése Az épület mint egységes szerkezet állékonysága A kitöltőfalazatok méretezése az épület állékonysága szempontjából Ferde dúcok, támaszok BefejezésülMegismételve azt, hogy a statikai tervezés igen komoly és felelősségteljes, emellett magas szintű szakképesítéshez kötött munka, a téma iránt érdeklődők számára nem felesleges a statikai méretezés fő vonalainak megismerése. Meg kell jegyeznem, hogy a mérnöki tudomány ezen ága igen száraz, és nehezen magyarázható el olyanok számára, akik alapvetően nem műszaki végzettségűek - de talán sikerülni fog... Statikai alapelvek laikusok számára Az épületek, építmények állékonyságának biztosítása, a megfelelő méretű és teherbírású szerkezetek megtervezése a statika - vagy szilárdságtan - tudomány feladata. Két fő része van: a mechanika (ez az alapelveket rögzíti) és a tartószerkezettan (mely már a konkrét szerkezeti számításokról szól). A mechanika tárgykörében a leendő építészek, építőmérnökök, statikusok és egyéb ilyen léhűtők a szilárd testek és - szükség esetén - a folyadékok, gázok azon reakcióit ismerik meg, melyek a teste belső erőinek, vagy külső erő hatására keletkeznek. Ennek legegyszerűbb esete, amikor egy - a nagyságával és az irányával meghatározott - erő hat egy testre. Minden mechanikai, statikai számítás ezen az alapesten nyugszik. Ettől kezdve aztán már valahol a végtelenben a lehetőségek határa: a test lehet rögzített, elmozduló, alakja, formája az egyenestől a többszörösen törtig, vagy a szépen íveltig - lehet konzolos és két végén alátámasztott, és így tovább, és így tovább. A ráható erő is lehet ilyen-olyan-amolyan irányú, hathat egyszerre több irányból, lehet megoszló - de lehet akár dinamikus is. Ez a gyönyörű szakma - a statikus szakma - a fenti lehetőségek végtelen számú variációját ismeri, dolgozza fel, számítja ki - és ha valamilyen módozata a fenti lehetőségeknek nem lenne ismert - kitalálja magának... De mi az, a mi ezek közül minket érdekelhet? Először is nézzük a tárgyakat - talán ez az egyszerűbb. Az épületbe épített szerkezetek lehetnek tömbösek, rúdszerűek és felületek. Tömbszerű például egy alaptest. A rúdszerűek közé a gerendák és oszlopok tartoznak, míg felületszerűek a falazatok, födémek. E szerkezeteknek van önsúlya, és vannak olyan belső erői, melyek mindenképpen hatással vannak szilárdságtani mutatóikra. A statikán belül ezekkel a belső tulajdonságokkal csak a folyamat befejezésekor (bizonyos ellenőrzések elvégzéséhez) foglalkozunk, egyébként számításainknál egységes, minden pontján, minden felületén azonos tulajdonsággal rendelkező testként számolunk velük. Itt kell megjegyezni, hogy az általam igen kedvelt és hangsúlyozottan előnyben részesített vályogfalak, földfalak esetében ez az álláspont csak igen-igen nagy fenntartásokkal tartható. De erről a megfelelő helyen szólok is. Tehát ismerjük a testeket, alkotórészeket, melyekkel foglalkozni szeretnénk. A testekre ható erők már egy kicsit bonyolultabbnak tűnnek, bár ha valaki emlékszik még középiskolás fizikai tanulmányaira, annak megérthetőek lesznek a következő mondatok. Ha valaki mégsem emlékszik, akkor remélem felidézi ezen fejezeteket az ötödikes-hatodikos tankönyvekből... Az erőket irányukkal és nagyságukkal jellemezzük: Szerkesztéskor, számításkor egy nyílban végződő egyenessel - vektorral - jelöljük. A nyíl mutatja az erő irányát. Ha geometriai eljárással kívánjuk a számítást is elvégezni, akkor az erőket méretarányosan jelöljük.
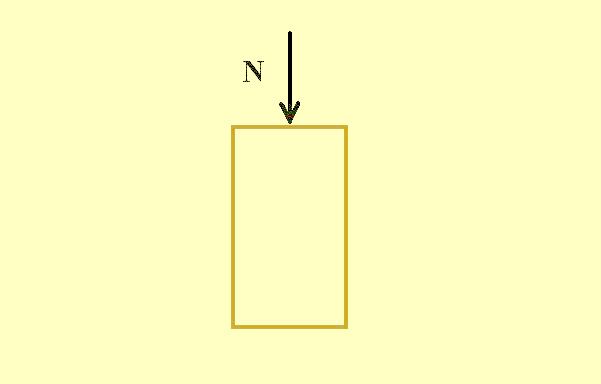
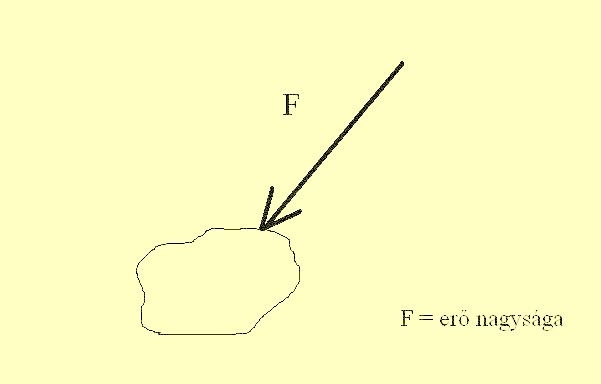 Erővektor ábrázolása A legegyszerűbb erő a nyomó erő, mely a testet a föld középpontja felé nyomja - mely tulajdonképpen maga a gravitációs erő. Mivel egy szerkezetnek - a gravitáció okán - önsúlya is van, bizonyos erő már hat rá külön terhelés nélkül is. Ha pedig valamit fölé helyezünk, valamit tartania is kell: az már az erők összeadódását jelenti. Mivel a test - általában - egy szilárd testen áll (ami maga a föld, avagy épületeknél az alap), a nyomóerő összeszorítani igyekszik a testet. Egy puha papírdoboz erre a hatásra valóban össze is nyomódik - a beton alaptest nem - no jó: ha becsületesen van elkészítve... A nyomóerő legismertebb és leggyakoribb formája a függőleges lefelé ható erő - mely a gravitációból ered.A tárgyak, testek méretezésénél ezzel az erővel igen gyakran kell foglalkoznunk. Ennek oka, hogy az építésben a különféle tartóknak, épületszerkezeteknek legtöbbször a saját és a felettük elhelyezkedő épületrészek súlyát kell hordozniuk. A nyomóerő jele a statikában egységesen egy nagy N betű.
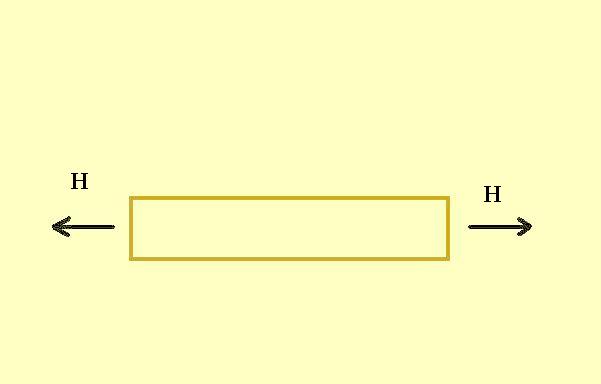
 Nyomóerő Húzóerő A húzóerő a test elemeit, részeit egymástól elhúzza, széthúzza. A nyomóerőnek ellenálló testek, tárgyak általában a húzóerőt is jól visleik - bár gyakori, hogy nagyságrendekkel kisebb húzóerőt bírnak el. Erről a szilárdságtani táblázatok magyarázatánál részletesebben olvashatsz.
 Húzás A hajlítóerő a legbonyolultabb - de végül is a fenti két erőből származtatható. Ha egy test egyik oldala húzást szenved, a másik nyomást: a testre hajlítóerő hat.
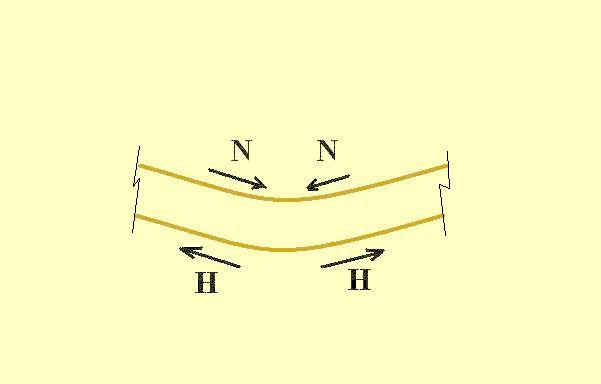 Hajlítás A nyomaték Ha egy olyan testre, szerkezetre, melynek egyik vége rögzített, a másik szabadon elfordulhat, valamilyen erő hat, akkor azt az erőt nyomatéknak nevezzük. A nyomaték nagysága a hatóerő nagyságától és a rögzítéstől való távolságától függ. Elsősorban az egyik végén befogott szerkezetek lehetnek jó példák erre (ilyenek az erkélykonzolok), de a folytonos alátámasztás nélküli tartóknál - azaz a tartógerendáknál - is számolni kell a nyomatéki erőkkel.
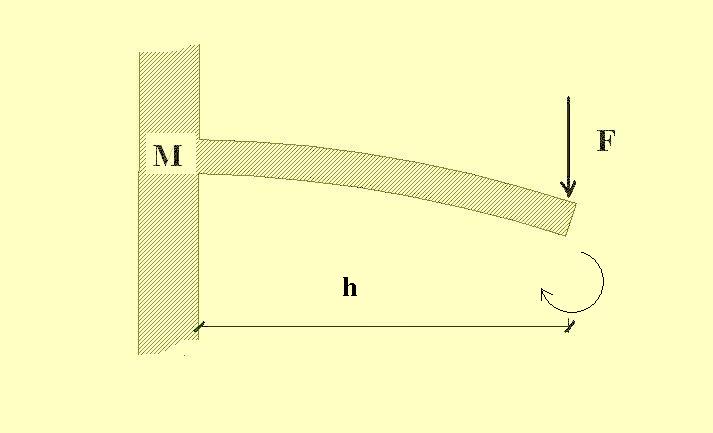 Nyomaték A tartó tövénél keletkező nyomaték nagysága az erő és az erőkar szorzatából számítható ki- M= F . h Az erővel kapcsolatban fontos tudnivaló, hogy az lehet pontszerű,és lehet megoszló. Az erő iránya fontos ismérv, és különféle állékonysági mutatók (pl. nyírás, kidőlés) miatt számításainknál nem lehet kihagyni. Általában függőleges és vízszintes erőkkel számolunk, ha ferde erőről van szó, akkor azt - a vektorszerkesztési szabályok alapján - vízszintes és függőleges elemeire bontjuk. A testek viselkedése erők hatására A testek az erők hatására különféle elváltozásokat szenvednek. A méretezés épp arra irányul, hogy a testek olyan módon (méretben, anyagból) legyenek kialakítva, hogy elbírják a terheket. Minden testnek van egy olyan határértéke, melyen túl a terhelést nem bírja el. Ezt a határértéket több minden befolyásolja, ezek közül a legfontosabbak: maga a test minősége (anyaga), a test geometriai méretei (hosszúsága, keresztmetszete), valamint az, hogy milyen módon vannak alátámasztva, befogatva. Itt kell beszélni egy, a tartószerkezettanban igen fontos körülményről, a testek keresztmetszeti kialakításáról. Végezzünk el egy kísérletet. Egy gyufásdobozt fektessünk az asztalra, és nyomjuk be felülről. Láthatjuk, hogy kis erő hatására a doboz összelapul. Ha azonban a dobozt a hosszabbik élére állítjuk, már jóval nagyobb erő kell az összenyomásához, ha pedig a rövidebbik élére, akkor kézzel szinte nem is tudjuk összenyomni. Pedig ugyanarról az anyagról - papírról - van szó. (Jó, megengedem, van egy kis csalás a kísérletben, hisz a gyufásdoboz egy dobozszerkezet, melynek az egyszerű testtől némileg eltérő szilárdságtani tulajdonságai vannak - de azért szemléltetésnek megfelel.) Láthatjuk tehát, hogy egy adott keresztmetszeti méretekkel rendelkező tárgy másképp viselkedik az erőhatásokkal szemben, ha a rövidebbik, másképp, ha a hosszabbik lapját terheljük. Ezt a jelenséget keresztmetszeti tényezőnek nevezzük - nevében hordozza, hogy a tárgy keresztmetszetétől függ. Ezek után nem kell külön bizonyítani, hogy egy különböző magassági és szélességi mértetekkel rendelkező test - azaz tartószerkezet - akkor bír el nagyobb terhet, ha az erő irányával a hosszabbik oldala párhuzamos. Azaz egy függőleges erőt az a gerenda jobban bír tartani, melyet rövidebb élére állítva helyezünk alá, mint egy olyan, melyet a hosszabbik élére fektetve.
A keresztmetszeti tényező kiszámítása a statikai méretezés alapművelete. Módját minden szakembernek ismernie kell, és nagyon régóta megvannak már azok a táblázatok is, melyek az előforduló legfontosabb keresztmetszetek ilyen tényezőjét (inerciáját) tartalmazzák.
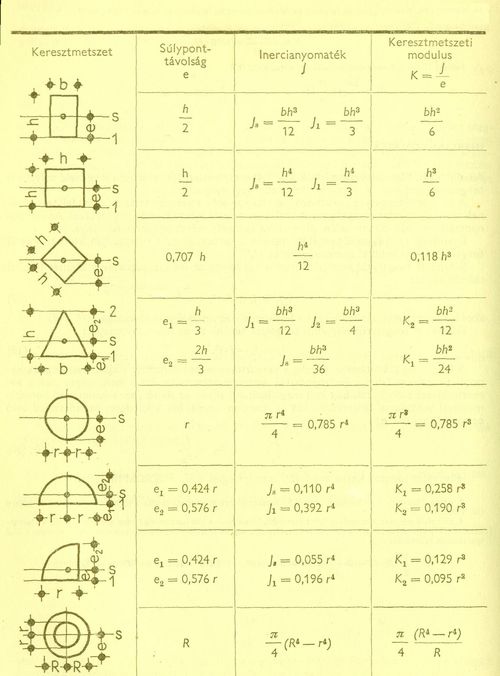 Különféle keresztmetszetek jellemzői Később majd látjuk, hogy ez igen fontos megállapítás a tartók méretezése szempontjából. Elemek szilárdsága, határfeszültségek Ahogy háromféle erőről szóltunk az előbb, háromféle határszilárdságot kell figyelembe venni az anyagok méretezésénél. A testek nyomóerő hatására összenyomódnak, feszültség keletkezik bennük. Ez a feszültség abból ered, hogy a test részecskéi egyre közelebb kerülnek egymáshoz. Ám van egy határ, amin túl már nem tudnak jobban "tömörülni" - efölött a testek károsodnak, eltörnek. Ezért is nevezték régen az ilyen erőhatást törőhatárnak. Sok test igen nagy nyomóhatárértékkel rendelkezik - ezek egytől-egyig alkalmasak építőanyagnak. A kő, a tégla, a fa e tulajdonsága miatt lehetett évezredek óta hasznos építőanyag. A húzóerővel szembeni határszilárdság általában kisebb, mint a nyomóerőé, ám vannak olyan szerkezetek - és anyagok - melyeknél a húzószilárdság a nagyobb. Húzás hatására a testek részecskéi egymástól eltávolodnak - mint a gumiszalag, amikor feszítjük. Léteznek olyan testek, melyek húzás hatására eredeti alakjuk, hosszuk akár többszörösére megnyúlhatnak anélkül, hogy tönkremennének, ám vannak, melyek ezt a hatást nehezen viselik. Ez utóbbiak közé tartozik például a vályog. A nyomatéki erő a testet elfordítani igyekszik stabil helyzetéből. Ha a test nincs fixen rögzítve, ez meg is történik: elfordul, ledől. Ám ha a test rögzítve van (szakzsargonban ezt úgy nevezik: befogott), akkor a nyomatéki erő hatására magában a testben keletkeznek feszültségek. Legegyszerűbb esetben - ahogy azt a hajlításról szóló ábra is mutatja - a hatóerő felőli oldalon húzás, az azzal ellentétes oldalon nyomás.
E hajlítóerő ismerete, az anyagok, testek reagálásának felismerése és számítása az építészetben az ún. vízszintes tartóknál (azaz vízszintes vagy ferde gerendáknál, födémeknél) lényeges. Ez az erő felel ugyanis a tartók behajlásáért, a vele szembeni ellenállás határozza meg, hogy mennyi terhet tud elviselni a szerkezetünk. A vékonyabb keresztmetszetű tárgyak, vagy azok, melyek ridegebb anyagból készülnek, kevésbé alkalmasak hajlítóerő hordására. Míg a fémek általában jól viselik a hajlítást, a fa már kevésbé, a kő és téglaanyagok pedig igen kis hajlítószilárdsággal rendelkeznek. A hajlítás számításánál igen fontos szerepet játszik az adott test, adott tartó keresztmetszeti tényezője, melyről korábban már szóltam. Ezen felül a különféle erők vagy erőegyüttesek hatására más módon is válaszolhatnak a testek - az épületek szerkezetei. A nem kellően rögzített elemek oldalerő hatására kifordulhatnak, a nem megfelelő súlyú, vagy nem a megfelelő pontban, módon terhelt elemek kidőlhetnek - és még számos ilyen hatás léphet fel. A statikai számítások előírásai, a vonatkozó szabványok természetesen ezekre is tartalmazzák az előírásokat - de most ezekkel ne foglalkozzunk. Ha valakit érdekelnek e konkrét problémák, legcélszerűbb szakemberhez fordulni. A testekben keletkező feszültségeket a szakemberek - régóta felállított egységes alapelvek szerint - grafikus ábrákon, úgynevezett belső erő ábrákon ábrázolják. Belső erőnek azért nevezik, mert a mechanika elméleti alapjai szerint a teste képzeletben elvágják, és a megmaradó testdarab belsejében fellépő feszültségeket határozzák meg.
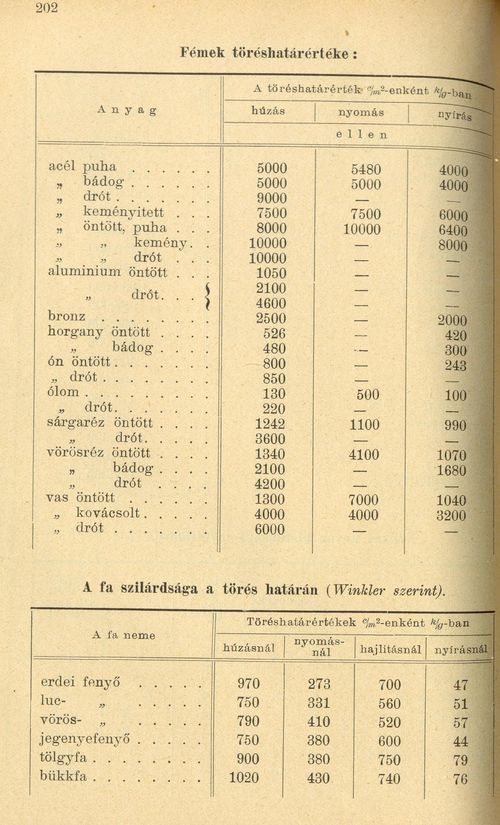
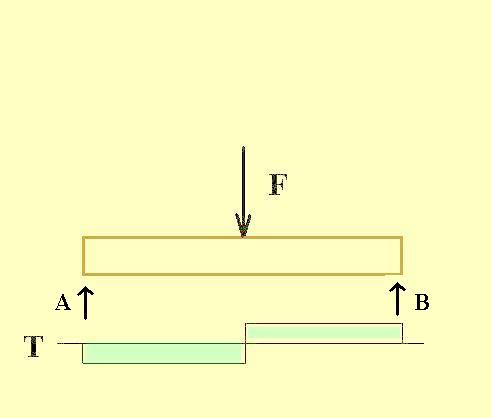 Két végén alátámasztott tartó nyíróerő (T) ábrája koncentrált teher esetén 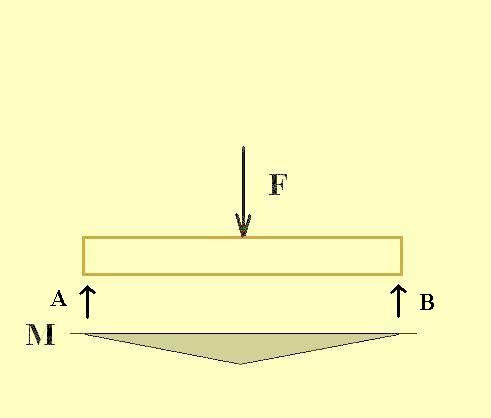 Két végén alátámasztott tartó nyomatéki ábrája (M) koncentrált teher esetén A belsőerő ábrák lényege, hogy a tartók, elemek fontos, lényeges helyén (keresztmetszetében) kiszámítjuk az egyes terhelési nagyságokat és azokat grafikusan ábrázoljuk. Egyszerű tartóknál, mint például egy koncentrált erővel terhelt födémgerendánál belsőerők így alakulnak: középen hat a gerendára a teher, míg két végén - az alátámasztásoknál - ennek tart ellen két erő. Ebben az egyszerű esetben könnyű meghatározni az ellentartó rőt: A is és B és egyenlő a teher felével. Amennyiben a szerkezetet több erő terheli, vagy megoszló teher van rajta, vagy a tartó nem két, hanem több helyen van alátámasztva, ez a számítás már bonyolultabb - számtalan variációs lehetőség van. A belsőerőábrák közül bemutatok néhányat a leggyakoribb esetekkel.
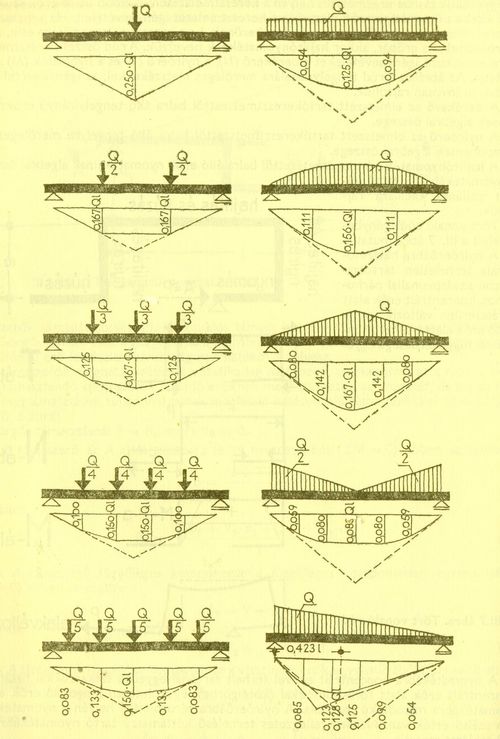 A fenti ábrák egyenes, kéttámaszú - azaz a két végén alátámasztott - tartót mutatnak be természetesen léteznek több támaszú tartók is, tört vagy ívelt vonalúak. Ezek belsőerő ábrái jóval bonyolultabbak, mint az itt is látható - de ezekkel most ne foglalkozzunk.
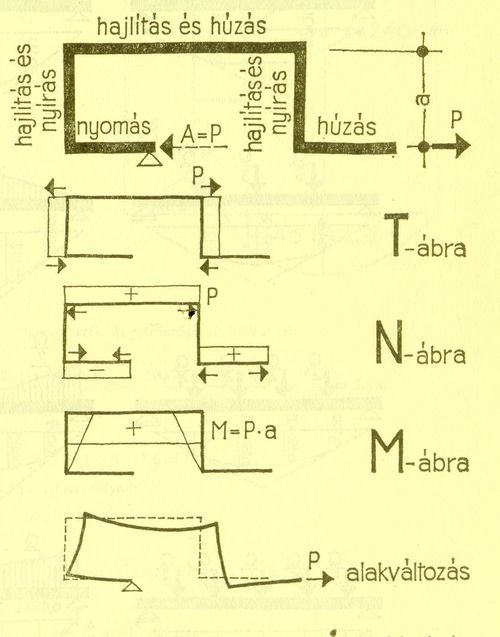 Rajz egy többször tört tartóról Az ábrák pontosan megmutatják azt az erőhatást (mértékét, irányát), melyek alapján a szerkezet méretezhető. Az erők, a testek erőkkel szembeni viselkedését tulajdonságokat az építéssel, építészettel foglalkozó tudósok, szakemberek évezredek óta tanulmányozzák, értékelik és persze használják fel eredményeiket. Már Vitruvius írt könyvében arról, hogy a nagy távolságokat áthidaló szerkezetként ne kőszerkezeteket, hanem fát kell használni. Az épületek falazatai, alapjai évszázadokon, évezredeken át vastag,tömör szerkezetek voltak - ez biztosította állékonyságukat. A gótika, majd a reneszánsz, végül a XIX. század technikai fejlődése - a vas megjelenése - vezetett az anyagok részletes szilárdságtani vizsgálatához, majd a matematikai, geometriai számítások bevezetéséhez. Ennek eredményeként megszülettek azok a szilárdságtani mutatók, melyeket végül is a mai kor szakemberei is alkalmaznak. Ezek közül a legfontosabbak az egyes anyagok szilárdsági határértékeit tartalmazó táblázatok. Az alábbiakban bemutatom a fa és a tégla nyomó-, húzó-, hajlítószilárdsági táblázatát, azért is, hogy legyen lehetőségünk összehasonlítani az adatokat.
 A fenti értékek - amint arról a faanyagok súlyát bemutató rész /itt/ is megmutatta - az évek során változtak, módosultak. Ennek igen egyszerű oka van: finomodtak a mérésükre szolgáló eljárások, bizonyos okok miatt egyszer-egyszer megengedőbb, máskor szigorúbbak lettek a szabályok (pl. a II. világháború alatt a nehézkes anyagbeszerzés miatt engedékenyebbek lettek egyes előírások). Statikai-tartószerkezeti számítások elmélete, menete Miután az anyagok, testek és az erők fő tulajdonságaival megismerkedtünk, nézzük, hogyan is történik egy épület elemeinek, tartószerkezeteinek méretezése. (Itt megint fel kell hívni a figyelmet, hogy az alant leírt dolgok csak az eljárás elméleti bemutatása, a tényleges számításkor rengeteg más körülményt is figyelembe kell venni - de hát ez már a szakemberek dolga.) Célszerűnek látom, hogy egy vázas szerkezetű épület elemeiről beszéljünk rögtön, hisz végül is ez az, ami minket érdekel. A statika - bármilyen bonyolult tudomány is - igyekszik minden feladatot a legegyszerűbb módozatra visszavezetni - ahogy az egyetemen ezt igen találóan kifejezték: a statikusok a világ leglustább emberei, mindig arra törekednek, hogy a lehető legkevesebb számítást kelljen elvégezni. Ezért hát - nagyon helyesen - minden tartószerkezetet, épületszerkezetet igyekeznek a legegyszerűbb formává transzformálni - és így már a legegyszerűbb módokkal el tudják végezni számításaikat. Miért van ez? Két ok miatt: ha valamilyen méretezésnél csak egyszerű, kevés matematikai műveletet kell elvégezni, akkor kevesebb a tévedési lehetőség - és ugye világos, hogy egy tartószerkezet téves tervezése milyen mérhetetlen károkat - esetleg baleseteket - okozhat. A másik ok szintén a lustaságra vezethető vissza: a statika mint tudomány kialakulásakor - valamikor a XIX. században még nem álltak a szakemberek rendelkezésére számítógépek, de még zsebszámológépek sem. Évtizedekig kézi szorzással, osztással, majd valamivel később a felejthetetlen logarléccel dolgoztak a statikus szakemberek. Csak egy megjegyzés: hiánypótló lenne e különös tárgy, csodaeszköz történetének, a műszaki haladásban játszott felbecsülhetetlen szerepének feltárása, megismertetése... No de e kis kitérő után nézzük épületünket.
A példaház
A példaház röntgenrajza
Felülről
A példaház váza
A példaház váza oldalról Milyen szerkezetek azok, melyek teherbírását meg kell terveznünk, hogy az épület valóban álljon? Sok-sok oszlop, A keretként szolgáló gerendák A födémet tartó gerendák A falak Mit is kell kiszámolnunk? Azt, hogy az adott terhelésekre az adott anyagból a felsorolt elemekként mekkorát kell beépítenünk ahhoz, hogy megtartsa a felette lévő szerkezetek terhét? Jelen esetben alapelvként rögzíthetjük, hogy a ház keretszerkezeteit fából, a kitöltéseket téglából kívánjuk elkészíteni. Ha nem rögzítjük ezt, akkor az előbbi célon - azaz az anyag méretén - túl az anyagtípus megfelelő kiválasztása is feladatunkká válik (pl. lehetne a gerenda vas, vagy vasbeton, a fal fa, kő vagy gipszkarton), de ezt most hagyjuk...
Mik azok az adatok, melyek rendelkezésre állnak a kiinduláskor? Az egyes elemek anyaga és hosszmérete. A keresztmetszeti méret még nem - hiszen éppen ezt fogjuk kiszámolni. A számítást általában fentről lefelé végezzük, hisz a terhek így jutnak egyre tovább. (Megjegyzem, van olyan lehetőség is, hogy alulról felfelé számítsunk, sok esetben ez a helyes mód, ám ekkor a feljebb lévő szerkezet méretváltozása esetén az alatt lévőt is újra kell méretezni. De ez gyakran előfordul például a közlekedésépítésben, amikor a burkolat vastagságának növekedése miatt újra kell számolni az alap adatait...) Most feltételezzük, hogy a tető már adott, megtervezett, ismert a súlya, mérete. Melyik hát az a szerkezet, melyet először méreteznünk kell? A födém, azon belül is a födémgerendák. Hisz ezek viselik a födém - és adott esetben a tető - súlyát.
 A födémgerendák a ház szerkezetében
A födém súlya könnyen kiszámítható: az alkotórészeket súlyát - mely azok vastagságától és anyagától függ - számba vesszük, összeadjuk. Igen ám, de a födémen teher is van - az úgynevezett hasznos teher. Ez lehet a bútorok súlya, lehet az ott közlekedő emberek súlya, nem egy esetben az ott tárolt dolgok (pl. faluhelyen a termények) súlya. A statikai tervezési szabályok már nagyon régóta ezeket a súlyokat csoportosították, táblázatba foglalták - hogy ne kelljen a számításokat végző embernek ezzel is idejét töltenie. Sőt - a szabványok kötelező hatállyal rögzítették is e számokat, így még egyszerűbb - és egységes is - a számítási módszer. Az alábbiakban egy ilyen súlytáblázatot mutatok be.
 A födémek méretezésénel figyelembe veendő terhek (Részlet egy 1904-es szakkönyvből)Ha megtaláltuk a megfelelő anyagot, súlyt, egyszerűen a födém felületével megszorozzuk, és megvan, hogy az adott födém kg terhet jelent az alatta lévő szerkezeteknek. Ezek pedig nem mások, mint a födémgerendák. És most jön a statikusok egyszerűségre törekvése. Az adott födémhosszt alá lehet támasztani egy marha nagy gerendával is középen - ám ez nem megoldás. Több kisebb méretű gerendát használjunk hát, ha a rendelkezésre álló tér megengedi, akkor 8-10 darabot. (Jó, itt azért van egy jegyzet a szabványok margóján: meghatározták ám, hogy mennyi lehet a gerendák maximális egymástól való távolsága, ez nagyjából 80-100 centi.) Tegyük fel, hogy mi a 100 centit, azaz egy métert választottuk ki (ennek lesz még jelentősége - kisebb távolság több gerenda, nagyobb távolság kevesebb, de erősebb gerenda - lásd majd e rész végén). És mit tesz ilyenkor az okos statikus? Van x számú gerendám. Felteszem, hogy a gerendák sorára egyenletes terhelés jut - azaz minden gerendára ugyanakkora. Akkor ezek szerint elég egy gerendát méreteznem, a többi ugyanolyan lehet. És mennyire igaza van! Csak nagyon extrém esetben kell eltérni ettől - például egy, a födém feletti koncentrált terhelésnél - mondjuk egy vastag válaszfalnál (erre szokták azt válaszolni a szakemberek: "födémre, főleg fa födémre nem teszek válaszfalat, koncentrált terhelést..."). Tehát csak egy gerendával kell foglalkoznom. De ennek hogyan tudom kiszámolni a keresztmetszetét? És itt jön a lényeg: lehet úgy is, hogy az erő nagyságának ismeretében kiszámítok egy kellő keresztmetszetet és ezt rögzítem. De a valóságban ez kicsit másképp történik - megfordítjuk az eljárást. Azaz meghatározom, hogy ide ilyen és ilyen keresztmetszetű gerenda kerül, és a számítás során ellenőrzöm, hogy ez megfelelő-e. Ha nem, növelem, vagy ha túl méretezett, csökkentem. Miért így végezzük ezt a feladatot? Azért, mert a tervezési munka során általában - és ez a helyes - az épület, az építmény alakja, szerkezete kerül elsőként megtervezésre. Azaz hogy milyen hosszú, milyen magas, milyen széles. És ez már adja az egyes elemek méreteit is. Innentől kezdve a statikusnak az a dolga, hogy igazolni tudja, hogy az adott méretű, anyagú szerkezet megfelel-e vagy sem. Igen nagy tervező vállalatoknál, vagy egy nagy, összetett, különleges épületnél a szerkezettervező és a statikus munkája (legtöbbször személye is) különválik. Ám gyakori - és ez sem helytelen megoldás - hogy a szerkezettervező és a statikustervező azonos személy, a két munkarész együtt, mindkét aspektust figyelembe véve folyik. Mert a szükséges módosítások ekkor követhetők a legegyszerűbben, nem történhet tévedés. De lépjünk tovább a számításban. Tehát ott tartottunk, hogy a tervező (építész) megálmodta, hogy a födém ekkora és ekkora méretű, ezt - esztétikai vagy éppen szerkezeti okokból - x számú gerendával akarja alátámasztani. Mint mondtam, csak egy gerendával kell foglalkoznunk, feltesszük, hogy a többi gerenda is ugyanezt a terhelést kapja. Hogy az adott tartógerenda méretének (esetleg anyagának) megfelelőségét meg tudjuk határozni, meg kell állapítanunk, hogy mekkora és milyen belső erők működnek a szerkezetben. De mik ezek a terhek, erők? A gerendára hat egy egyenletesen megoszló erő, mely nyírófeszültséget és nyomatéki feszültséget ébreszt a tartóban. Ez ered a gerenda önsúlyából, valamint abból, hogy rajta terhek fekszenek, melyek nyomják felületét. Fontos szempont, hogy a gerenda a két végén a falon ül, ezt nevezzük kéttámaszú tartónak. Nézzünk csak vissza az erőket bemutató ábrákra: jelen esetben nyomóerő - azaz a tartó hossztengelyével párhuzamos erő - nem keletkezik, így nyomóerőre nem kell méreteznünk a gerendát. Az erő nagysága kiszámítható egyszerűen: a rajta lévő terheknek súlya van, hozzászámoljuk a használati terheket. De mekkora terhet veszünk figyelembe, hiszen a gerenda mellett fut egy-egy másik is mindkét oldalán. Igen egyszerű a válasz. A gerendaközök távolságának felét vesszük mindkét oldalon, azaz ha gerendák 1 méterre vannak egymástól, akkor 50-50 centit (azaz egy métert).
Gerenda terhelése a födémmezőkkel Ennek alapján elkészíthetjük a nyíróerő ábrát és megállapíthatjuk, hogy a legnagyobb nyíróerő T kg. A nyírófeszültség egyenlő a nyíróerő és a nyírt felület hányadosával ( T/A ) A szabványokból, táblázatokból megvizsgáljuk, hogy ez a szám kisebb-e, mint az adott anyag - esetünkben egy fenyőfa gerenda - határfeszültsége.
Ha a megkapott eredmény kisebb, mint a határérték, akkor a gerenda megfelel. Ha nagyobb, akkor vagy a gerenda méreteit növeljük - de vigyázni kell, ilyenkor a gerenda önsúlya is nő, tehát újra kell számolnunk a terhelő súlyokat. A másik megoldás, hogy a terhelést csökkentjük - például más, könnyebb padlószerkezetet alkalmazunk. A gerendánkra nyomatéki erő is hat, mely hajlítani igyekszik azt. Ennek mértékét a már bemutatott nyomatéki ábra segítségével meg tudjuk határozni, majd kiszámíthatjuk a nyomatéki feszültség értékét. Ez annyiban különbözik az előző eljárástól, hogy itt nem a test keresztmetszetével, hanem annak keresztmetszeti tényezőjével számolunk. Ennek megfelelően a tartóban fellépő - és a nyomatékból eredő - feszültség = M / K Ezután nincs más feladatunk, mint megállapítani a határfeszültségeket tartalmazó táblázatból, hogy a tartóban fellépő feszültség (szigma -számított) kisebb-e, mint a megengedett határérték. Ha igen akkor a tartó megfelelő. A két feszültségszámítás (nyírási és hajlító) elvégzése után természetesen azt a keresztmetszetet kell alkalmaznunk tényleges, mely nagyobb - ez könnyen belátható. A fenti leírás természetesen igen-igen leegyszerűsítve mutatja be a folyamatot. A különféle terhelések, alátámasztások, az anyagfajták, a szerkezete méretei (pl. a karcsúság, melyről később még lesz szó) mind-mind befolyásolják a tartók méreteit. Vannak a méretezésnek más szempontjai is, mint például a lehajlás (ez esztétikai, vagy a más szerkezetekhez való kapcsolódás miatt lényeges), vagy a hőtani méretezés (a megfelelő hőszigetelés miatt). Előfordulhat, hogy ezek eredményeként a szerkezeten változtatni szükséges - ekkor a statikai tervezést, ellenőrzést újra el kell végezni. A szabályok, a méretezési előírások e tényezőket rögzítik, a szakemberek ezeket mind figyelembe veszik. Láthatjuk, hogy e számítások nem bonyolultak, sőt a szakemberek a különféle anyagokra már számtalanszor elvégezték őket. Ezért évtizedekkel ezelőtt számba vették, rendszerezték és táblázatba foglalták a méretezések eredményeit. A táblázatok tartalmazzák a tartók anyagfajtáit (beton, fa, vas), és a terhelések nagyságának valamint az áthidalandó távolságnak a függvényében meghatározzák a szükséges keresztmetszetet. Természetesen előfordulhatnak különleges esetek, ezért a számítási eljárás ismerete elengedhetetlen. De napjainkban ezeket már számítógépek végzik el pillanatok alatt. Nézzünk egy ilyen táblázatot - 1904-ből
Általános esetben egy tartó, egy gerenda két végén kerül alátámasztásra, és a két támaszték között csak a gerenda feszül. Ám a fachwerk épületek esetében van két olyan különleges és jellemző tényező, melyekről szintén szólnunk kell. Mi van akkor, ha a gerenda egyik vége túlnyúlik a támaszon (mint az a példaépület homlokzatán látható), vagy ha a gerenda alatt szilárd szerkezet (például fal, mint a fachwerk házaknál mindene esetben) található. Sokan megkérdezik tőlem, hogy miben különbözik a fachwerk ház más vázas (pl. a napjainkban igen elterjedt könnyűszerkezetes) házaktól. Ebben. Azaz nem csak a ház váza vesz részt a teherhordásban, hanem a falazat is. És ettől olyan erős a ház. Nézzük csak meg a túlnyúló gerenda esetét (melyet konzolnak nevezünk) A konzolos szerkezete csak egyik végükön befogottak, a másik - elméletileg - szabadon elfordul.
Konzolos tartók terhelési esetei
E szerkezeteknek mások a feszültségi viszonyai, amint azt az alábbi ábrákon láthatjuk - ám a statikai számítás menete ezeknél sem különbözik az előbb bemutatottnál. Ha a terhelések, a belső erők mértékét kiszámítottuk, a feszültségek, majd a szükséges méretek meghatározása már ugyanolyan egyszerű módon lehetséges, mint az egyszerű kéttámaszú tartónál. Kicsit bonyolultabb a példaépületünk esete, ahol a födémgerendák egyik vége felfekszik, a másik pedig konzolosan kinyúlik a végfalak fölé. De ez sem jelent megoldhatatlan problémát. Viszont az eredmény egy - a vázas épületek szerkezeti tervezésénél fontos - következtetésre vezet: az ilyen konzolosként túlnyúló tartók kisebb keresztmetszettel is meg tudják tartani ugyanazt a terhet, mint a kéttámaszú tartók. Ennek igazolását az alábbi belsőerőábra mutatja, de józan ésszel átgondolva is beláthatjuk ezt: a tartó két fal közötti részére jutó terhelés mintegy "ellen tart" a konzolos részt terhelő erőnek - nem engedi elfordulni a tartót. Ezt a tulajdonságát a konzolos tartónak a régi fachwerk házak építői régóta ismerték, és ki is használták. Ezért lehetett mód arra, hogy a régi házak emeletei kinyúljanak a földszinti falsík elé, ezzel jelentős többlettér alakulhatott ki. És persze az is előnyös volt, hogy vékonyabb, azaz olcsóbb faanyagot építhettek be a födémbe. Koszorúgerenda méretének számítása
A födémgerenda megtervezése után nézzük a következő szerkezetet lefelé haladva. Ez nem más, mint a faváz vízszintes keretét alkotó gerendázat - melyet sok helyen koszorúnak hívnak. (A koszorúgerenda napjainkban már más értelmet kapott, de mi maradunk ennél a kifejezésnél).
 A koszorúgerenda a ház szerkezetében
A gerenda méretezési elve nem különbözik az előzőtől, mindössze a terhelések és támaszok elosztása, mennyisége más. A rövidebbik falat felülről határoló koszorúgerendára példánkban öt darab födémgerenda ül fel. (A rajzon e gerendák és a koszorúgerenda egy síkban került ábrázolásra, de ez ne tévesszen meg senkit: a "szerkezeti megoldások" fejezetben bemutatott lapolásnak nevezett fakötés teszi lehetővé a gerendák egy síkban történő elhelyezkedését, de ettől még a felül lévő födémgerendák terhelik a koszorúgerendát). Ezen kívül még terhet jelenthet az épület oromfala is, ám most a számítás egyszerűsítése érdekében úgy vesszük, mintha ennek elenyésző súlya lenne (pl. egy vékony deszkaorom). Tehát a terhelési ábránkon öt - méghozzá egyforma - erő jelenik meg a koszorúgerendán, mely a két végén az épület sarokoszlopaira támaszkodik fel. Tehát számolhatunk úgy, mintha a már ismert kéttámaszú tartóval lenne dolgunk. Ebben az esetben egyszerű a feladatunk, a nyíróerő ábra és nyomatéki ábra így fest:
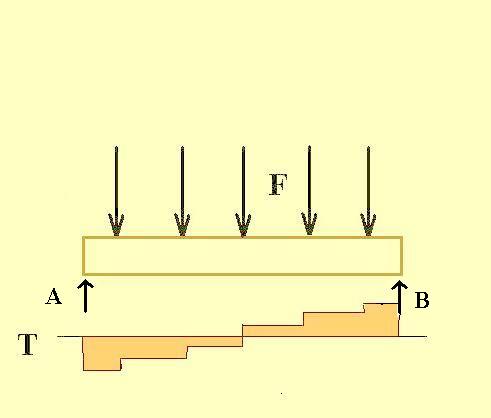 Nyíróerőábra 5 darab koncentrált teher esetén 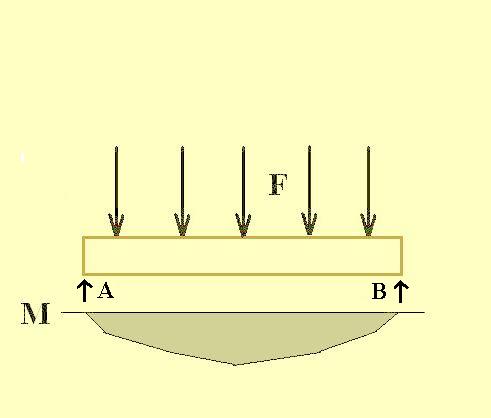 Nyomatéki ábra 5 darab koncentált erő esetén
Ezek alapján a már megismert módon kiszámítható a gerenda szükséges keresztmetszete. De nem csak a rövidebbik oldalon található koszorúgerendákat kell meghatároznunk, hanem a hosszabbik oldalon találhatókat is. Az eljárás már ismerős - odafigyelést csak az általuk tartandó teher meghatározása igényel. Példánkban e két hosszabbik gerendára támaszkodik fel a tetőszerkezet. Ennek súlya kiszámítható. A tetőteherhez hozzá kell számítani a hóterhet is, mely - mint az idei év katasztrófái bebizonyították - igen fontos tényező. A súlyok e gerendát terhelhetik egyenletesen megoszlóan (ha pl. külön szelemenek fogják össze a szarufákat), vagy pontszerűen több helyen (amikor a szarufák közvetlenül a gerendára ülnek fel). Mindkét terhelési esetre ismerjük már az eljárást, ezek szerint meghatározhatjuk ennek a koszorúnak a méreteit is.
Igen ám, de példánkban a koszorúgerendákat még alátámasztják oszlopok is. A rövidebb oldalon kettő darab, a hosszabbikon....darab. Megtehetjük, hogy ezen oszlopok tartóerejével is számolunk. Az eredmény az lesz, hogy kisebb keresztmetszetű gerenda is elegendő lesz, hiszen a terhelés nem kettő, hanem négy ( a hosszabbik oldalon ) felé oszlik el. Ez igen hasznos eredmény: hiszen ezzel csökkenthető a faanyag mérete - olcsóbbat is fel lehet használni. A közbülső alátámasztások lehetősége elsősorban a nagyobb fesztávolságot áthidaló gerendáknál lényeges: ezekkel megoldható az, hogy ne kelljen nagy méretű, drága - és nehezen kezelhető - szerkezeteket beépíteni.
De van itt valami, ami nem statikai probléma, inkább már a szerkezettervezés, magának az építészetnek a tárgykörébe tartozik. Mégpedig az, hogy figyelni kell arra, hogy egy összetett vázszerkezetben kedvezőtlen látványt nyújt és bizonytalanság érzetét kelti, ha egy tartógerenda mérete kisebb, mint a felett elhelyezkedő, arra terhelő gerendáé. Hiába tudjuk és igazoljuk számítással, hogy statikailag helyes a megoldás: ezt kerülni kell. A koszorúgerenda teherbírását (és ezzel) méretét azonban valami más is befolyásolja: a korábban egy fél mondatban már említett kitöltőfalazat. Ha ez a kitöltő falazat valamilyen könnyűszerkezet (igazi fachwerk épületeknél általában könnyűvályog), akkor ennek a tartószerepét nem lehet figyelembe venni. Más a helyzet a nehézvályog, vagy az égetett tégla kitöltőfalak esetében. Alapesetként meg lehet azt is tenni, hogy nem számolunk velük (ekkor a tartó a már ismert kéttámaszú tartó marad), de igazán jó - és szakmailag is kihívást jelentő - megoldás, ha a falak teherbírását is segítségül hívjuk a terhek viselésére. Ennek bemutatása azonban már nem fér bele e leírásba.... A faváz oszlopainak méretezése A gerendák kiszámítása után kell gondoskodnunk a függőlegesen álló oszlopok méretezéséről. A menet az előbbiekhez hasonló. Természetesen itt nem nyírással és hajlítással kell számolnunk, hanem a szerkezet hosszanti tengelyével párhuzamos nyomással. A nyomóterhek a rúdszerű szerkezetekre (például oszlopokra) rendszerint koncentráltan hatnak, ez egyszerűbb számítást eredményez. Gondot csak az jelenthet, ha a teher nem pontosan a szerkezet tengelyvonalában hat (úgy nevezik: külpontos), de ezzel most ne nehezítsük életünket. Az épület oszlopaira a koszorúgerendák által továbbított teher hat. Nagyságát könnyen ki lehet számítani. Grafikusan az erőt így ábrázolhatjuk:
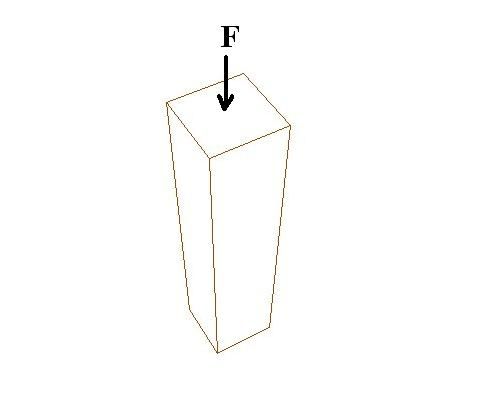 A terhelő erő nem más, mint a koszorúgerendák által átadott súly. Ennek kiszámítása úgy történik, hogy a koszorúgerendára jutó összes terhet (a rövidebbik gerendáknál a födém és a födémgerenda önsúlya, míg a hosszabbik oldalnál a tetőteher, és a gerenda önsúlya) összesítjük, majd elosztjuk négyfelé. Ehhez természetesen még hozzáadódik az oszlop saját súlya is, mely egy nagyobb keresztmetszetű faoszlopnál már nem kevés. Nézzük csak: A födémteher 250 kg=m2, az 5,0 méterszer 10,0 méteres házon ez 12500 kg. A tető feltételezzük, hogy - hóteherrel együtt - 5000 kg. A gerendák súlya könnyen kiszámolható a hosszukból és a fajsúlyukból: Födémgerendák: 5 db x 10 méter x 0,18 x, 0,22 1,98 m3 Koszorúgerendák: 2 x 5 méter, 2 x 10 méter = 40 méter 40 méter x 0,2 x 0,25 = 2,00 m3 A lucfenyő számítási súlya: 600 kg/m2 600 x 3,98 = 2388 kg összesen: 19888 kg Négy felé osztva ez: 4972 kg Az oszlop önsúlya: 3 m x 0,25 x 0,25 x 600 112 kg együtt: 5084 kg Az oszlopban fellépő feszültség kiszámítása egyszerű feladat. A terhelőerőt elosztjuk a támadott felület nagyságával, és a megkapott eredmény az a feszültség, melyet össze kell hasonlítanunk a fa határfeszültségével. 5084 kg/25 x 25 cm = 8,13 kg/cm2 Az összehasonlításnál azonban nagyon kell figyelnünk arra, hogy a meglévő feszültségi táblázatokból melyik értékre is van szükségünk. Nézzük csak közelebbről a tartóoszlopot: a fagerendák - mert az oszlop nem más, mint egy függőlegesre állított gerenda - szálai hossztengelyével párhuzamosan futnak. Maga a teher is e tengellyel párhuzamos, amint az ábrából láthatjuk. Tehát az ennek megfelelő határértékkel kell számolnunk. Miért fontos ez? Mert mint a táblázat mutatja, a fának a szilárdsági tulajdonságait - sok más anyaggal ellentétben - jelentősen meghatározza, hogy a támadó erő milyen irányból hat. Eddig igen egyszerű a feladat, ám most jön az a tényező, ami nehézzé teszi az ilyen szerkezetek szerkesztését. Azon testek, melyek magassági mérete meghaladja - általában - a szélességük vagy a vastagságuk kétszeresét, hajlamosak a felülről támadó erők hatására kitérni. Igaz ez a falazatokra ugyanúgy, mint az oszlopszerű szerkezetekre is. A kitérés lehet eldőlés, elborulás, vagy lehet hajlás, kihajlás. Tapasztalat, hogy az ilyen építési szerkezetek - anyagjaik tulajdonságai miatt - a nyomóerőnek minden további nélkül ellent tudnak állni, ám teherbírásukat jelentősen csökkenti karcsúságuk. A téglafalazatoknak a nyomószilárdsága például elképesztően nagy, de közismert, hogy egy két méternél magasabb falazat igen könnyen kiborul. A kihajlásban, a dőlésben szerepet játszanak a tartót közvetlenül terhelő erők, de felléphetnek más erők is. Ezek közül az egyik az úgynevezett szélteher, amikor az oldalirányból fújó szél igyekszik kimozdítani helyéből a falt, az oszlopot. A másik a tartó ún. külpontos nyomásából származik. Nézzük csak az ábrát:
A külpontos nyomás magyarázata Nyomaték ('M') = erő ('F') . erőkar (ez esetben 'r')Láthatjuk, hogy a külpontos - azaz nem a keresztmetszet mértani központjában ható - nyomóerő egyben nyomatékot is ébreszt a tartóban. Ha az ilyen erő a keresztmetszet súlypontjától túlságosan távol esik, akkor elmozdítani - azaz kidönteni - igyekszik a tartót. Ez a probléma nem csak oszlopoknál áll fenn, hanem igen súlyos következményekkel járhat a falazott szerkezeteknél (kő-, tégla-, vályog-, földfalaknál) is. Ezek ugyanis elsősorban a stabilitásukkal összefüggő teherbírásuk révén hordják a terheket - ha a stabilitás nem biztosított, akkor a súlyok tartására sem képesek. E fontos ténynek a figyelmen kívül hagyása (pl. a falak mellett, alatt végzett földmunkák, a falak egyes részeinek meggondolatlan kibontása) vezet sajnos gyakran végzetes balesetekhez, a falak leomlásához. Ezekkel a körülményekkel a statikusoknak számolniuk kell, nem lehet figyelmen kívül hagyni őket. A figyelembevételükre, a velük történő számításra pontos előírások vannak, ezeket be kell tartani. Természetesen ehhez a feladathoz is rendelkezésünkre állnak ma már táblázatok, útmutatók, de egyszerű képletek is. Az alábbiakban például a fatartók kihajlásának vizsgálatára szolgáló képleteket és táblázatokat ismerhetjük meg a XX. sz. elejéből. Az elvek és a fő számítási mód azóta sem változott...
Eljutottunk tehát az oszlopokig. Már csak a talpgerendák és a falak méretezése van hátra. A fachwerk házak talpgerendái két terhet viselnek: a sarkukra állított oszlopok terhét és a kitöltések falazatanyagának terhét.
Talpgerenda és oszlopok a ház szerkezetében Mivel feltételezzük, hogy a talpgerendák - a modern előírásoknak megfelelően - végig alaptestre vannak fektetve, bennük hajlítóerő nem lép fel. Ezzel szemben nyíróerő igen - méghozzá jelentős mértékű nyíróerő az oszlopok alatt. De ezek kiszámítása, majd az általuk okozott feszültség meghatározása már nem okozhat gondot az előzőekben megismertek alapján. A talpgerendák esetében még két igen fontos tényezővel számolni kell. Az egyik a kifordulás, a másik a pecsétnyomás.
A kifordulásnak lehet oka maga a gerenda magassági mérete is, de leginkább az okozza, hogy a talpgerendához rögzített oszlopra különféle oldalirányú erők hatnak (pl. a már említett szél). A kifordulás ellen a talpgerendát biztosítani kell, ezt legtöbbször az alaphoz történő csavarozással oldják meg. Ám az erővel számolni kell, és igazolni szükséges, hogy talpgerendánk alkalmas felvételére.
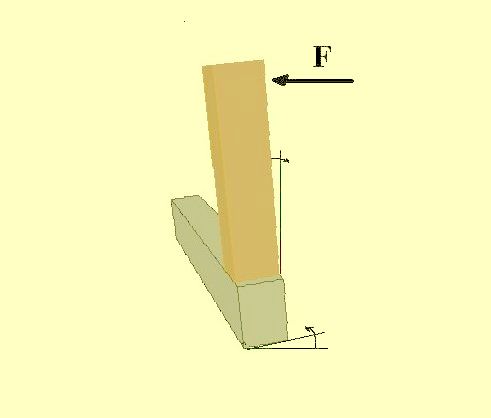 A mereven összekapcsolt oszlop és talpgerenda kifordulása oldalirányú erő hatására Pecsétnyomás akkor keletkezik, ha egy nagyobb felületen egy kisebb felületű szerkezet helyezkedik el, és azt egyenletesen, az egész érintkező felületén nyomja. Vannak anyagok, melyek igen érzékenyek a pecsétnyomásra, nem tudnak ellenállni vele szemben. Ezek közé tartoznak például a vályogfalak, földanyagú szerkezetek, de egyes fák is. Elsősorban a puhafáknál kell a pecsétnyomásból eredő károsodással számolni.
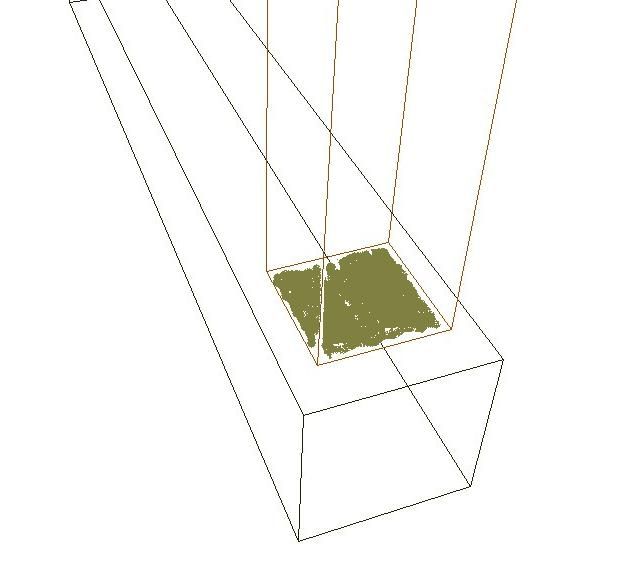 Az úgynevezett "pecsétnyomás" A pecsétnyomás számításakor a nyomóerőt kell figyelembe venni, majd az ennek a révén fellépő feszültséget a határfeszültséghez viszonyítani. Ám itt megint figyelni kell: most nem a rostokkal párhuzamos, hanem az azokra merőleges határfeszültséget kell figyelembe venni. Napjainkban a falazóanyagok, falazatok méretezése már nem is a statikai állékonyság igazolására szolgál (hisz a felhasznált anyagok állékonysága bizonyított), hanem inkább a hőszigetelési, esetleg állékonysági (azaz kidőlés elleni) tulajdonságaik bizonyítására. Természetesen igen fontos a különféle erők számbavétele, nem szabad elfelejtkezni az oszlopok esetében már említett egyéb körülményekről sem (kidőlés, külpontos erőhatás stb.). A téglafalakban, vályog- és kőfalakban a nyomások gúla ill. kúpszerűen terjednek, a terjedési irány az anyagfajtától függ, de nagyjából a 30 fokos szöget zár be. A falak szilárdságát nem maga a fal anyaga, hanem az együttes szerkezet, azaz a habarcsrétegekkel egymáshoz között elemegyüttes adja. Épp ezért a falazatok szilárdsága jóval alacsonyabb,mint az azt alkotó egyes elemeké. A határfeszültséget éppen ezért a habarcsminőség függvényében adják meg. Például a téglafalak határszilárdsága a gyengébb (H4) habarcs esetében 7 kg/cm2, míg a legerősebb H200-as habarcsnál 26-30 kg/cm2 is lehet. A falazatok méretezése rutinfeladat, hőszigetelés bizonyítása pedig nem a statikus dolga. Az épület mint egységes szerkezet állékonysága Feltétlenül szólni kell arról, hogy nem csak favázas épületünk egyes elemei, de maga az egész épület minden alkatrészével együtt ki van téve mindenféle erőhatásoknak, és ezeknek ellent kell állnia.
Vegyük csak elő újra kis gyufásdobozunkat, de most a gyufákat vegyük ki belőle. Játszunk el egy kicsit velük. Állítsunk össze ragasztó segítségével egy egyszerű teste: egy kockát. Ha ragasztó megszáradt, a kockát letéve nagyszerűen megtartják magukat a szálak. De próbáljuk csak oldalról megnyomni az egyik gyufaszálat - vagy felülről ráhelyezni valamilyen nehezebb tárgyat - mondjuk stílszerűen egy hamutartót. A keretes váz nem fogja elviselni a behatást. Az első esetnél függőleges elemei - az oszlopok - elferdülnek, a nyomás irányával párhuzamos szálak eltolódnak helyükről. Súly hatására legtöbbször - a függőleges szálak ferdén elhajlanak, és amelyik először szenvedi el ezt a hatást, annak a környezetében a felső keretet alkotó szálak megrogynak, a ragasztó hatását legyőzve elválnak egymástól: épületünk összerogy. Mindeközben maguk a szálak semmit nem károsodnak, nem törnek el. Ha nem is látjuk, nem is tapasztaljuk, vázas épületeinkkel is ez történik - legyenek azok akár vasbeton vázzal épültek, akár favázasak. Amint azt az előzőekben már megismerhettük, az egyes elemek szilárdsága viszonylag könnyen és jól kiszámítható, igazolható. A vázas épületek elemei önmagukban, egyenként természetesen megfelelnek a statikai előírásoknak - ám vázszerkezetként, együttesen már más szempontokat is figyelembe kell venni velük kapcsolatban. De hogyan lehet ezt a hatást mérni, feldolgozni, és hogyan lehet ezek ellen megvédeni épületünket? (Ez az építészet, a tartószerkezettan egyik legszebb ága, a legnagyobb felkészültséget igénylő problematikája.) Jelen kis írás nem alkalmas arra, hogy részleteiben bemutassa az ilyen erőhatások működését, a számítások menetét. Ha valakit részletesebben érdekel a téma, szakirodalomban, szakkönyvekben megtalálhatja tudományos feldolgozását. A házakra, épületekre is jellemzően két erő: a függőleges nyomás (súly) és a vízszintes kimozdító erő (leggyakrabban a szél ereje) hat. Legnagyobb gondot az jelent, ha e két erő együtt lép fel.
Vázas szerkezeteink esetében a fő probléma az, hogy a káros alakváltozásokat okozó hatások eredményként egyetlen elem megsérülése, vagy a rendeltetésszerű helyzetétől való eltérése magával hozza a kapcsolódó szerkezetek károsodását is. Míg egy tömör téglafal, vagy egy gerendás födém esetében az egyik részének megrongálódása (pl. leomlása) nem jelenti azt, hogy a további részek is tönkremennek, a vázas falaknál ez szinte elkerülhetetlen. A kísérletből láthattuk, hogy két fő csoportja lehet a károsodásoknak: az egy-egy falmezőt határoló rudak elmozdulása, illetve a csomópontok károsodása. Mindkét problémával a statika, a szerkezettan kimerítően foglalkozik. Itt most csak a lényegét tudom leírni a tudnivalóknak, javaslom, akit részleteiben érdekel, az akár a net-en, akár a szakirodalomban nézzen utána. Elsőként az egymáshoz kapcsolt rúdelemek (azaz a váz) elmozdulásának megakadályozásáról. Erre a célra az épített falazatok azon tulajdonságait használjuk ki, hogy a vékonynak mondható szerkezet lapsíkkal párhuzamos ellenálló képessége - azaz ha egy falat "élén" terhelünk - igen nagy. Jóval magasabb, mint például az oldalirányú ellenállása. (rajz: rajz x). Így ez egy igen merev testet alkot, ami alkalmas az oldalirányú terhek ellen állni. Ehhez természetesen úgy kell a falakat beépíteni, hogy szoros kapcsolat alakuljon ki köztük és a faváz között. Ennek fizikai megoldásairól a szerkezetekről szóló fejezetben olvashatunk. Fontos még, hogy a falak építésük után bizonyos süllyedést szenvednek. Ezt elkerülendő a favázas falak mezői 2 méternél ritkán magasabbak. A kitöltőfalazatok méretezése az épület állékonysága szempontjából A probléma megoldása statikusi ismereteket igényel. Ha érdekel a téma, szakkönyvek, tanulmányok tucatjait megtalálhatod erről. A net-en például nagyon hasznos ismereteket olvashatsz Halmágyi Lóránt: Kitöltőfalakkal merevített vázak számítása című írásában. Megoldások lényege, hogy a nyírási tönkremenetel a falazóelemek közötti kötőrétegekben - azaz a fúgákban -, a falmező középső szakaszán jöhet létre. A fal ellenállása a falazat minőségétől függ. A falazatnak az átlóra merőleges irányú húzással szembeni ellenállása nehezen mérhető, számítható - épp ezért elég bizonytalan. Kísérletek szerint nagyjából a falazat (tehát nem a falazóelemek, hanem a komplett falazat) nyomószilárdságának tizedére tehető. A vázas szerkezetek másik fő problémája a váz-csomópontok merevségének biztosítása. Erről az alábbi ábrát érdemes megtekinteni: Eleink hamar rájöttek ennek szükségességére, és természetesen gondoskodtak a sarkok és az egymást keresztező, vagy egymáshoz csatlakozó vázrudak kitámasztásáról.
A támasztékok méretezése annyival bonyolultabb, hogy ezekben - mivel ferdén állnak - az erők bizonyos szögben lépnek fel. Egyébiránt nem bonyolultabb szerkesztésük, bár a teherbírásukat erősen befolyásolja az oszlopokhoz, gerendákhoz való kötésük módja. Épp ezért általában nem csak magát az elemet, hanem a kötést kell méretezni, mert ez lehet a leggyengébb része a merevítésnek. A méretezési eljárás a többtámaszú, merevített tartók (más néven: rácsos tartók) méretezését jelenti - ez a tartószerkezettan egyik legbonyolultabb fejezete. Gyakran a számításokkal, szerkesztésekkel megjelenített belsőerőábrák már meg is jelenítik a tartók kialakításának sémáját - ezért az egyik leglátványosabb statikai műveletnek nevezhető méretezésük. A régiek gyakran használtak kissé görbe fákat a ferde támaszokhoz: ezeknél ugyanis a görbeség megfelelően elhelyezve - azaz felfelé ívesen - boltívként működött és erősítette a rendszert. Itt tehát nem volt hátrány a görbe fa, melyet gerendáknál, oszlopoknál nem lehetett volna ezeket felhasználni, de itt igen. A ferde támaszok, dúcok keresztmetszeti mérete legtöbbször a megtámasztott elemével egyezett meg, ez a falazat látványa miatt is célszerű volt. Figyelemre méltó, hogy az Unióban bevezetésre váró, a fatartók méretezéséről szóló EUROCODE 5-ös tervezési irányelv már különfoglalkozik a merevítőelemek méretezésével is. Miután a favázas épületek minden egyes elemét így kiszámoltuk, érdemes visszatekinteni a már bemutatott 1904-es táblázatra. Szomorúan jövünk rá: a táblázatok, a régi korok gyakorlatán alapuló meghatározások a sok-sok számítás eredményével nagyjából megegyező eredményt hoztak. Azon kívül, hogy nincs új a nap alatt, rájöhetünk arra, hogy elődeink sem voltak butábban nálunk. Persze ma már egy tervezés, egy engedélyezés során nem lehet arra hivatkozni, hogy "az 1904-es szakkönyv ezt a méretet írta elő" - de jó tudni, hogy a tudomány igazolja a sok évszázados tapasztalatot... Érdekes adalék: a II. világháború idején már rendelkezésre állt (sőt, előírásként is napvilágot látott) több olyan segédlet, ami felgyorsította, megkönnyítette a tartószerkezettervezést. Nem véletlen ez. Szükség volt a döntések gyors meghozatalára, és igen gyakran nem képzett statikusok, mérnökök, hanem alacsonyabb képzettségű emberek feladata lett az épületek, építmények megtervezése, megalkotása. Egy példa ebből az időből: a nyomott faoszlopokban megengedhető legnagyobb igénybevételek meghatározása:

Látható, egy egyszerű számítással (a terhelő súlyokat elosztjuk a keresztmetszettel, és a táblázatból a karcsúságnak megfelelő értékkel összehasonlítjuk) eldönthető, a tervezett tartó megfelel-e. Példánkban ez így fest: A karcsúság: 300 cm / 25 cm = 12. Mivel puhafáról van szó, a táblázat szerint a feszültség maximális értéke 49 kg/cm2 lehet. Az általunk korábban számított feszültség értéke 8,13 kg/cm2. Tehát megfelel...
|
Ha valami érdekel, esetleg segítségre van szükséged: